ANSWER
4,410
Step-by-step explanation
The number of ways we can choose 4 teachers from 7 teachers is,
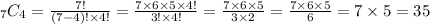
There are 35 ways of choosing 4 teachers out of 7.
And the number of ways we can choose 4 students from 9 students is,
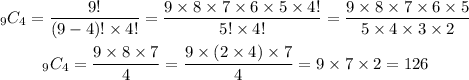
There are 126 ways of choosing 4 students out of 9.
The committee is formed by 4 teachers and 4 students. The number of ways it can be made is,

Hence, there are 4,410 ways to choose 4 students and 4 teachers out of 9 students and 7 teachers.