Given the following parameter:
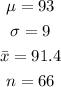
Using z-score formula
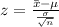
Substitute the parameter provided in the formula above
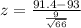
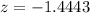
The probability that the mean monitor life will be greater than 91.4 is given as
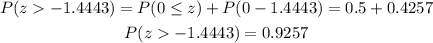
Hence, the probability that the mean monitor life will be greater than 91.4 months is 0.9257