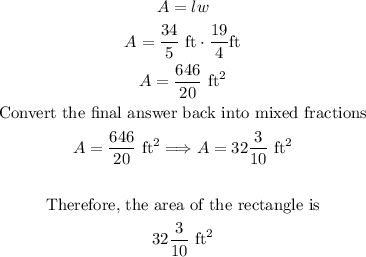Recall the area of a rectangle is determined by the formula

Given the following
w = 4 3/4 ft
l = 6 4/5 ft
Convert the following given into improper fraction first
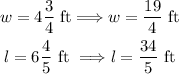
Next, substitute those values to the given formula for solving the area of the rectangle