We have that the line passes by the points (0, -2) & (1, 2). Using this we determine the slope (m) and then the function. After that we transformate the function. We proceed as follows:
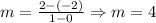
Now, using one of the points [In our case we will use (0, -2), but we can use any point of the line] and the slope, we replace in:

Then:
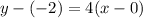
Now, we solve for y:
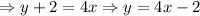
And we apply the transformation to our line, that is f(x) -> f(x) + 6:
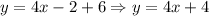
Therefore our final line (After the transformation) is y = 4x + 4, and graphed that is: