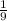Solution:
Remember the following formula :
P(AUB) = P(A)+P(B)-P(AnB)
According to the data of the problem and applying the previous equation, we obtain the following equality:

This is equivalent to:

solving for P(A n B), we get:

so that, we can conclude that the correct answer is: