The decay of this radioactive unknown compound is a first-order process.
We can express the time dependence of its mass m using a first-order integrated rate law, where k is the rate constant:
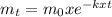
mt = mass at time t
m0 = initial mass
t = time
-----------------------------------------------------------------------------------------------------
Procedure:
1) We need to find "k":
From the first-order rate law we clear k,
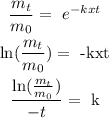
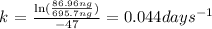
----------------------------------------------------------------------------------------------
2) We find the half-life from the value of k we have just calculated:
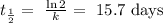
-----------------------------------------------------------------------------------------------
3) The number of half-lives of the unknown sample is:
Number of Half-lives = 47 days / 15.7 days = 3 (approx.)
Answer: Number of half-lives = 3