Question

A 695.7 ng sample of an unknown radioactive substance was placed in storage and its mass measured periodically. After 47 daysthe amount of radioactive substance had decreased to 86.96 ng. How many half-lives of the unknown radioactive substancehave occurred?

Answer 1

The decay of this radioactive unknown compound is a first-order process.

We can express the time dependence of its mass m using a first-order integrated rate law, where k is the rate constant:

`m_t=m_0xe^(-kxt)`

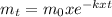
mt = mass at time t

m0 = initial mass

t = time

-----------------------------------------------------------------------------------------------------

Procedure:

1) We need to find "k":

From the first-order rate law we clear k,

`\begin{gathered} (m_t)/(m_0)=\text{ }e^(-kxt) \\ \ln ((m_t)/(m_0))=\text{ -kxt} \\ (\ln ((m_t)/(m_0)))/(-t)=\text{ k} \end{gathered}`
`k\text{ = }(\ln ((86.96ng)/(695.7ng)))/(-47)=0.044days^(-1)\text{ }`

----------------------------------------------------------------------------------------------

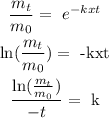
2) We find the half-life from the value of k we have just calculated:

`t_{(1)/(2)}=\text{ }(\ln 2)/(k)=\text{ }15.7\text{ days}`

-----------------------------------------------------------------------------------------------

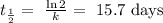
3) The number of half-lives of the unknown sample is:

Number of Half-lives = 47 days / 15.7 days = 3 (approx.)

Answer: Number of half-lives = 3