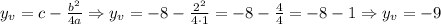We know that, for a parabola, the minimum, or the maximum, is given by the vertex of the parabola. The formula for the vertex of the parabola is given by:
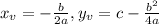
And we have the coordinates for x and y for the vertex.
We can see that the line of symmetry is x = -1, and this is the same value for the value of the vertex for x-coordinate, that is, the x-coordinate is equal to x = -1.
With this value for x, we can find the y-coordinate using the given equation of the parabola:

We can also expand these two factors, and we will get the same result:
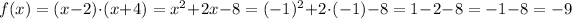
Therefore, the value for the y-coordinate (the value for the y-coordinate of the parabola, which is, at the same time, the minimum point for y of the parabola) is:
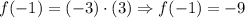
The minimum point of the parabola is (-1, -9) (answer), and we used the given function (rule) to find the value of the y-coordinate.
We can check these two values using the formula for the vertex of the parabola as follows:
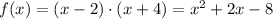
Then, a = 1 (it is positive so the parabola has a minimum), b = 2, and c = -8.
Hence, we have (for the value of the x-coordinate, which is, at the same time, the value for the axis of symmetry in this case):
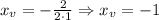
And for the value of the y-coordinate, we have: