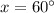Hello there. To solve this question, we'll have to remember some properties about trigonometric functions and the right triangle.
We want to find x such that:
![\tan (x)=\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1ephzp9e6ovfzx4yt2svpnysnckwy0iigz.png)
We'll use the second right triangle to show what we want.
First, given a triangle:
We know that the hypotenuse will be:
![\sqrt[]{x^2+y^2}](https://img.qammunity.org/2023/formulas/mathematics/high-school/e9w0zzbiiojc55bl3317k9l8a9055l0ego.png)
But most importantly, the tangent of the angles α and β can be calculated by only using the legs of the triangle: it is the ratio between the opposite side and the adjacent side to an angle.
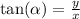
and
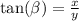
Now look at the triangle we have:
We can easily check that:
![\sqrt[]{3}=\frac{\sqrt[]{3}}{1}](https://img.qammunity.org/2023/formulas/mathematics/high-school/cdj3xxo3to5pt0b2aybmeggazgihxhug34.png)
So it would be good to find something that relates the ratio between those two numbers: the tangent of 60º!!
Therefore, we have:
![\tan (60^(\circ))=\frac{\sqrt[]{3}}{1}=\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/32pmaodoerfawqmqp4smgp5ievu1st6k45.png)
And the solution to x is: