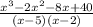We are given the following expression
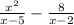
Let us re-write the expression as a ratio of polynomials p(x)/q(x)
First of all, find the least common multiple (LCM) of the denominators.
The LCM of the denominators is given by
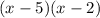
Now, adjust the fractions based on the LCM
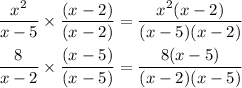
So, the expression becomes

Now, apply the fraction rule

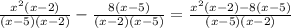
Finally, expand the products in the numerator
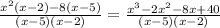
Therefore, the given expression as a ratio of polynomials p(x)/q(x) is