Question

The path of the baseball follows the equation h= -4.9t^2 + 60t + 1.5 where h represents the height of the baseball, t seconds after the baseball was hit. How long will it take the baseball to return to the ground?

Answer 1

Given the question in the question tab, the following are the steps to solve the problem:

Step 1: Write out the equation for the path of the baseball where h is height and t is time in seconds

`h=-4.9t^2+60t+1.5`

Step 2: Rewrite the new equation

The height of the baseball when it returns to the ground is zero(0). Therefore, at that point where the baseball returns to the ground, the function becomes:

`0=-4.9t^2+60t+1.5`

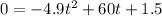
Step 3: We solve the quadratic equation to get the value of t:

`\begin{gathered} 0=-4.9t^2+60t+1.5 \\ u\sin g\text{ quadratic formula which states that:} \\ x=(-b\pm√(b^2-4ac))/(2a) \\ a=-4.9,b=60,c=1.5 \\ \text{Substituting the values, we have:} \\ \frac{-60\pm\sqrt[]{60^2-4(-4.9)(1.5)}}{2(-4.9)} \\ =\frac{-60\pm\sqrt[]{3600+29.4}}{-9.8} \\ =(-60\pm60.2445)/(-9.8) \\ =(-60+60.2445)/(-9.8)\text{ or }\frac{-60-_{}60.2445}{-9.8} \\ =(0.2445)/(-9.8)or(-120.2445)/(-9.8) \\ t=-0.024948979\text{ or }12.26984184 \\ t\approx-0.0249\text{ or 12.270} \end{gathered}`

Since the value for time cannot be negative, hence the time it will it take the baseball to return to the ground is approximately 12.270 seconds