Question

Consider the circle x ^ 2 + y ^ 2 = 100 and the line x + 3y = 10 and their points of intersection (10, 0) and B = (- 8, 6) . Find coordinates for a point C on the circle that makes chords AB and AC have equal length . Be sure to justify your answer.

Answer 1

The equation of circle is given by,

`x^2+y^2=100\text{ ---(1)}`

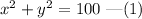
The equation of line is given by,

`x+3y=10\text{ ---(2)}`

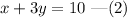
The points of intersection of the circle and line is,

A=(Xa, Ya)=(10, 0)

B=(Xb, Yb)=(-8, 6)

The length of chord AB can be calculated using distance formula as,

`\begin{gathered} AB=\sqrt[]{(X_b-X_a)^2+(Y_b-Y_a)^2} \\ =\sqrt[]{(-8-10)^2+(6-0)^2} \\ =\sqrt[]{(-18)^2+6^2} \\ =\sqrt[]{324+36} \\ =\sqrt[]{360} \\ =6\sqrt[]{10} \end{gathered}`

Let (Xc, Yc) be the coordinates of point C on the circle. Hence, using equation (1), we can write

`X^2_c+Y^2_c=100\text{ ---(3)}`

Using distance formula, the expression for the length of chord AC is given by,

`AC=\sqrt[]{(X_c^{}-X_a)^2+(Y_c-Y_a)^2_{}}`

Since (Xa, Ya)=(10, 0),

`\begin{gathered} AC=\sqrt[]{(X^{}_c-10_{})^2+(Y_c-0_{})^2_{}} \\ AC=\sqrt[]{(X^{}_c-10_{})^2+Y^2_c} \end{gathered}`

It is given that chords AB and AC have equal length. Hence, we can write

`\begin{gathered} AB=AC \\ 6\sqrt[]{10}=\sqrt[]{(X^{}_c-10_{})^2+Y^2_c} \end{gathered}`

Squaring both sides of above equation,

`\begin{gathered} 360=(X^{}_c-10_{})^2+Y^2_c\text{ } \\ (X^{}_c-10_{})^2+Y^2_c=360\text{ ----(4)} \end{gathered}`

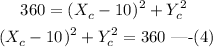
Subtract equation (4) from (3) and solve for Xc.

`\begin{gathered} (X^{}_c-10_{})^2-X^2_c=360-100 \\ X^2_c-2* X_c*10+100-X^2_c=260 \\ -20X_c=260-100 \\ -20X_c=160 \\ X_c=(160)/(-20) \\ X_c=-8 \end{gathered}`

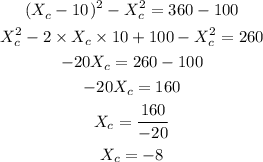
Put Xc=-8 in equation (3) to find Yc.

`\begin{gathered} (-8)^2+Y^2_c=100 \\ 64+Y^2_c=100 \\ Y^2_c=100-64 \\ Y^2_c=36 \\ Y^{}_c=\pm6 \\ Y^{}_c=6\text{ or }Y_c=-6 \end{gathered}`

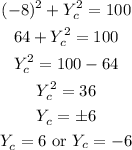
So, the coordinates of point C can be (Xc, Yc)=(-8, 6) or (Xc, Yc)=(-8, -6).

Since (-8, 6) are the coordinates of point B, the coordinates of point C can be chosen as (-8, -6).

Therefore, the coordinates of point C is (-8, -6) if chords AB and AC have equal length.