We will have the following:
*First: We have that the equation of the circle will be given by:

Here (h, k) is the coordinate of the center of the circle and r is the radius of the circle.
*Second: We will replace the center of the circle and determine the radius:
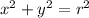
*Third: We determine the radius of the circle by using the point given:
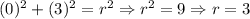
*Fourth: We have the following expression representing the circle:
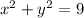
So, we replace the point (-2, sqrt(5)) to determine whether or not it belongs to the circle, that is:
![(-2)^2+(\sqrt[]{5})^2=9\Rightarrow4+5=9\Rightarrow9=9](https://img.qammunity.org/2023/formulas/mathematics/college/g5au1p0lo0r9hqcoj9rqnnlhl04rzbwly1.png)
Thus proving that the point (-2, sqrt(5)) does lie in the circle.