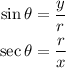
Given the conditions in the question:
1. sin θ > 0, therefore, it must be positive. From that, we can conclude that y must be on the positive side, therefore, located at the top of the coordinate plane.
2. sec θ < 0, therefore, it must be negative. From that, we can conclude that x must be on the negative side, therefore, located at the left side of the coordinate plane.
Therefore, the quadrant that the θ belongs to is in the top and left of the coordinate plane and that is Quadrant II.