Question

Given the median QR and trapezoid MNOP, what is the value of X?M3.8033Rکد 73PA. 6B. 19(C. 2D, 5E 7F. Cannot be determined

Answer 1

Consider the diagram below

Applying the rule in the diagram above, we have

`|QR|=(1)/(2)(|ON|+|PM|)`

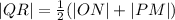
Recall from the questions

`\begin{gathered} |QR|=33 \\ |ON|=3x-8 \\ |PM|=7x+4 \end{gathered}`

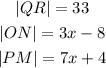
Then we substitute the parameters above into the expression above

`\begin{gathered} 33=(1)/(2)(3x-8+7x+4) \\ \text{ Multiply both sides by 2} \\ 66=3x-8+7x+4 \\ \text{rerrange the terms and simplify } \\ 66=10x-4 \\ \text{collect like terms } \\ 66+4=10x \end{gathered}`

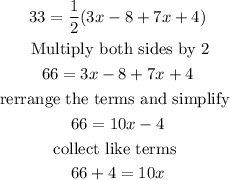
simplify further

`\begin{gathered} 70=10x \\ \text{divide both sides by 10} \\ x=(70)/(10) \\ \text{then} \\ x=7 \end{gathered}`

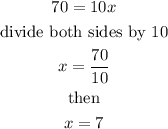
Therefore the value of x is 7

Therefore the right option is E