Question

1) If a horizontal asymptote exists for this function, identify its location.4x + 6x3x3 - 2x + 1AyoB3B) y =4OyD Does Not Exist

Answer 1

For this problem, we are given the following rational function:

`f(x)=(4x^3+6x)/(3x^3-2x+1)`

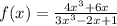
We need to determine the horizontal asymptote for this function. In order to determine this, we need to calculate the limit of the function when x approaches infinity. We have:

`\lim_(x\rightarrow\infty)(4(\infty)^3+6\cdot\infty)/(3(\infty)^3-2\cdot\infty+1)=(4)/(3)`

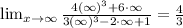
The horizontal asymptote exists at y= 4/3. The correct option is C.