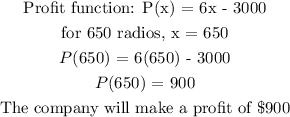Question

The graph above shows the graph of the cost in blue and revenue in red function for a company that manufactures and sells small radios.ABCD

Answer 1

a) 500 radios

b) Going out = $5000

Coming in = $5000

c) P(x) = 6x - 3000

d) Profit of $900

Step-by-step explanation:

a) To get the number of radios that must be produced to break even, we will equate the cost function and the revenue function:

`\begin{gathered} \cos t\text{ function:} \\ C(x)\text{ = 3000 + 4x} \\ \text{revenue function:} \\ R(x)\text{ = 10x} \\ \\ \text{Break even:} \\ C(x)\text{ = R(x) } \\ \text{3000 + 4x = 10x} \end{gathered}`

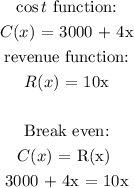
collect like terms:

`\begin{gathered} 3000\text{ = 10x - 4x} \\ 3000\text{ = 6x} \\ \text{divide both sides by 6:} \\ x\text{ = 3000/6} \\ x\text{ = 500} \\ \text{If x represents number of radios produced,} \\ \text{Then to break even, 500 radios will have to be produced } \end{gathered}`

b) The dollar amount going in and coming out is gotten by replacing the value of x in both function with 500:

`\begin{gathered} \text{when x = }500 \\ C(x)\text{ = 3000 + 4x = 3000 + 4}(500) \\ C(x)\text{ = }5000 \\ \text{Amount going out = \$5000} \\ \text{when x = 500} \\ R(x)\text{ = 10x = 10(500)} \\ R(x)\text{ = 5000} \\ \text{Amount coming in = \$5000} \end{gathered}`

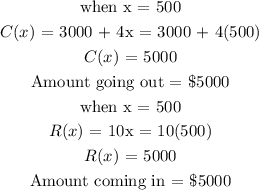
c) Profit = Revenue - Cost

`\begin{gathered} \text{Profit function, }P(x)\text{= R(x) - C(x)} \\ P(x)\text{ = 10x - (3000 + 4x)} \\ P(x)\text{ = 10x - 3000 - 4x} \\ P(x)\text{ = 6x - 3000} \end{gathered}`

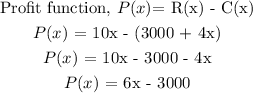
d) To find the profit when the number of radios is 650

`\begin{gathered} \text{Profit function: P(x) = 6x - 3000} \\ \text{for 650 radios, x = 650} \\ P(650)\text{ = 6(650) - 3000} \\ P(650)\text{ = 900} \\ \text{The company will make a profit of \$900} \end{gathered}`