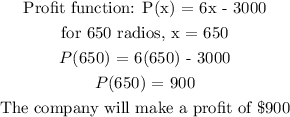a) 500 radios
b) Going out = $5000
Coming in = $5000
c) P(x) = 6x - 3000
d) Profit of $900
Step-by-step explanation:
a) To get the number of radios that must be produced to break even, we will equate the cost function and the revenue function:
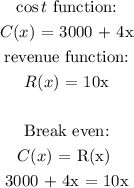
collect like terms:

b) The dollar amount going in and coming out is gotten by replacing the value of x in both function with 500:
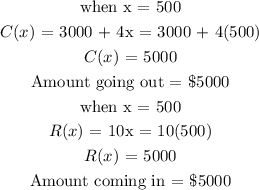
c) Profit = Revenue - Cost
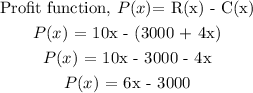
d) To find the profit when the number of radios is 650