Question

A 2 kg ball is dropped from a height of 60 m. Find its speed just before it hits the ground. Assume no friction. Answer​

Answer 1

`\huge\sf\red{A}\pink{N}\orange{S}\green{W}\blue{E}\gray{R}`

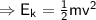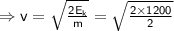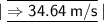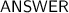
Given,

mass of the ball, m=2 kg ;

height of the ball, h=60 m

The initial potential energy of the ball,

`{\boxed{\underline{\sf{E_(p)=m g h=(2)(10)(60)=1200 \mathrm{~J}}}}`

When the ball reaches the ground, its potential energy becomes zero as it is entirely converted into its kinetic energy (
`{\sf{E_(K)` ), i.e.,

`{\Rightarrow{\sf{E}_{\sf{k}}=1200 \mathrm{~J}}}`

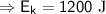
If v is the velocity attained by the ball just before reaching the ground,

`{\Rightarrow{\sf{E}_{\sf{k}}=(1)/(2){mv}^(2)}}}`

`{\sf\Rightarrow{v=\sqrt{\frac{2 \sf{E}_{\sf{k}}}{\sf{m}}}=\sqrt{(2 * 1200)/(2)}}`

`{\Large{\mid{\underline{\overline{\Rightarrow{\sf{34.64\:m/s}}}}\:{\mid}`

Answer 2

-34.3m/s

Step-by-step explanation:

first lets find the time befor it hit the ground by using free fall equation and we know we use that in one condition which is a constant acceleration in this case its a gravitational acceleration which is -9.8

`h = (1)/(2) g {t}^(2)`

`t = \sqrt{ (2 * 60)/(9.8 ) } = 3.5s`

now we know that the initial velocity its zero :

so applu the another kinematic equation which is

`v = u - gt`

v is final velocity and u is the initial velocity and its equal zero.

v = - 9.8 × 3.5 = - 34.3