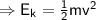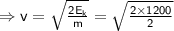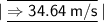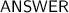
Given,
mass of the ball, m=2 kg ;
height of the ball, h=60 m
The initial potential energy of the ball,
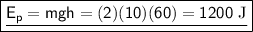
When the ball reaches the ground, its potential energy becomes zero as it is entirely converted into its kinetic energy (
 ), i.e.,
), i.e.,
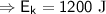
If v is the velocity attained by the ball just before reaching the ground,