Given:
Distance of top of ladder to the ground = 10 ft
Distance of bottom of ladder from the side of the house = 9 ft
Let's find the length of the ladder.
Since the ladder forms a right triangle with the house, to find the length of the ladder apply Pythagorean Theorem.
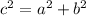
Where:
a = 10 ft
b = 9 ft
c = length of ladder
Thus, we have:
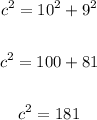
Take the square root of both sides:
![\begin{gathered} \sqrt[]{c^2}=\sqrt[]{181} \\ \\ c=13.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/oqcz1gl4e3rsg41l6ywayk0jypoj6crbhl.png)
Therefore, the length of the ladder rounded to the nearest tenth is 13.5 ft
ANSWER:
13.5 ft