Given the equation system:

The first step is to replace the first equation in the second equation
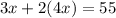
With this, we have a one unknown equation. Now we can calculate the value of x:
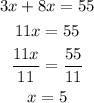
Now that we know the value of x, we can determine the value of y, by replacing x=5 in the first equation
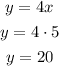
This system has only one solution and that is (5,20)