Let d and s be the cost of a double and single- occupancy room, respectively. Since a double-occupancy room cost $20 more than a single room, we can write
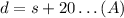
On the other hand, we know that 15 double-rooms and 26 single-rooms give $3088, then, we can write
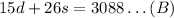
Solving by substitution method.
In order to solve the above system, we can substitute equation (A) into equation (B) and get
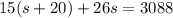
By distributing the number 15 into the parentheses, we have
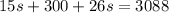
By collecting similar terms, it yields,

Now, by substracting 300 to both sides, we obtain
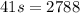
then, s is given by
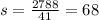
In order to find d, we can substitute the above result into equation (A) and get
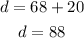
Therefore, the answer is:
