The coordinate of point X which is 5/6 of the distance between P and Q is 5/11
Here, we want to calculate the coordinates of point X which is 5/6 of the distance between P and Q
Mathematically, we can use the internal division formula.
In this case, the coordinates of y is 0 in all cases
So the coordinates of P is (-5,0) while the coordinates of Q is (7,0)
Now, the coordinates of X divides the line PQ in the ratio 5 to 6
Using the internal divison formula, we have;
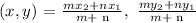
In this case however, we are going to focus on the x-axis part of the question since the values of y at all points is 0
m , n are the division values which are 5 and 6 respectively in this case
x2 is 7 while x1 is -5
Substituting all of these, we have;
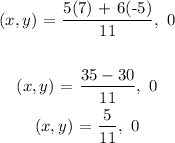
So the coordinate of point X which is 5/6 of the distance between P and Q is 5/11