Question

The radioactive isotope 14C has a half-life of approximately 5715 years. Now there are 50g of 14C.(1) How much of it remains after 1600 years? (Round your answer to three decimal places.)

Answer 1

We know that the amount of matter is given by:

`N=N_0e^(-\lambda t)`

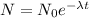
where λ is the decay constant. The decay constant is related to the half-life of the element by the equation:

`\lambda=\frac{\ln2}{t_{(1)/(2)}}`

Then we can express our first equation as:

`N=N_0e^{-\frac{\ln2}{t_{(1)/(2)}}t}`

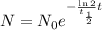
Plugging the initial amount, 50 g, the half-life of 5715 years and the time we want to know we have that:

`\begin{gathered} N=50e^{-(\ln2)/(5715)(1600)} \\ N=41.181 \end{gathered}`

Therefore, after 1600 years there are 41.181 g