Answer:
(a) P = 0.0167
(b) P = 0.9833
(c) P = 0.0093
Step-by-step explanation:
To answer these questions, we will use the binomial distribution because we have n identical events (13 households) with a probability p of success (27% still have a traditional phone landline). So, the probability that x families has a traditional phone landline can be calculated as
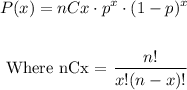
Replacing n = 13 and p = 27% = 0.27, we get:
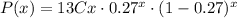
Part (a)
Then, the probability that no families have a phone landline can be calculated by replacing x = 0, so
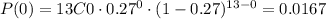
Part (b)
The probability that at least one family has a phone landline can be calculated as
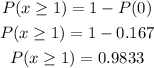
Part (c)
The probability that at least eight families have a phone landline can be calculated as
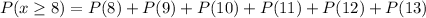
So, each probability is equal to
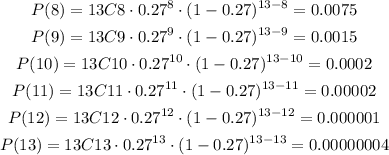
Then, the probability is equal to
P(x≥8) = 0.0093
Therefore, the answers are
(a) P = 0.0167
(b) P = 0.9833
(c) P = 0.0093