Question

Suppose that 27 percent of American households still have a traditional phone landline. In a sample of thirteen households, find the probability that: (a)No families have a phone landline. (Round your answer to 4 decimal places.) (b)At least one family has a phone landline. (Round your answer to 4 decimal places.) (c)At least eight families have a phone landline.

Answer 1

(a) P = 0.0167

(b) P = 0.9833

(c) P = 0.0093

Step-by-step explanation:

To answer these questions, we will use the binomial distribution because we have n identical events (13 households) with a probability p of success (27% still have a traditional phone landline). So, the probability that x families has a traditional phone landline can be calculated as

`\begin{gathered} P(x)=nCx\cdot p^x\cdot(1-p)^x \\ \\ \text{ Where nCx = }(n!)/(x!(n-x)!) \end{gathered}`

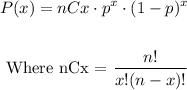
Replacing n = 13 and p = 27% = 0.27, we get:

`P(x)=13Cx\cdot0.27^x\cdot(1-0.27)^x`

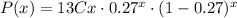
Part (a)

Then, the probability that no families have a phone landline can be calculated by replacing x = 0, so

`P(0)=13C0\cdot0.27^0\cdot(1-0.27)^(13-0)=0.0167`

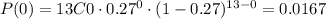
Part (b)

The probability that at least one family has a phone landline can be calculated as

`\begin{gathered} P(x\ge1)=1-P(0) \\ P(x\ge1)=1-0.167 \\ P(x\ge1)=0.9833 \end{gathered}`

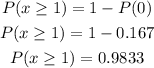
Part (c)

The probability that at least eight families have a phone landline can be calculated as

`P(x\ge8)=P(8)+P(9)+P(10)+P(11)+P(12)+P(13)`

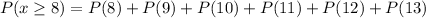
So, each probability is equal to

`\begin{gathered} P(8)=13C8\cdot0.27^8\cdot(1-0.27)^(13-8)=0.0075 \\ P(9)=13C9\cdot0.27^9\cdot(1-0.27)^(13-9)=0.0015 \\ P(10)=13C10\cdot0.27^(10)\cdot(1-0.27)^(13-10)=0.0002 \\ P(11)=13C11\cdot0.27^(11)\cdot(1-0.27)^(13-11)=0.00002 \\ P(12)=13C12\cdot0.27^(12)\cdot(1-0.27)^(13-12)=0.000001 \\ P(13)=13C13\cdot0.27^(13)\cdot(1-0.27)^(13-13)=0.00000004 \end{gathered}`

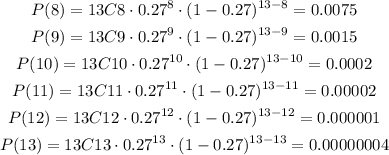
Then, the probability is equal to

P(x≥8) = 0.0093

Therefore, the answers are

(a) P = 0.0167

(b) P = 0.9833

(c) P = 0.0093