Given:
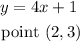
To find:
Draw a graph of a line that is perpendicular to the given line and passing through a given point.
Step-by-step explanation:
As we know that relation between two slopes of perpendicular slopes of lines:

Slope of given line y = 4x + 1 is:

So, the slope of line perpendicular to given line is:
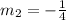
Also, so line equation that is perpendicular to given line is:
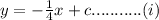
Also, the required line is passing thorugh given point (2, 3), i.e.,
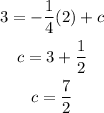
So, line equation that is perpendicular to given line is:
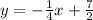
The required graph of line is: