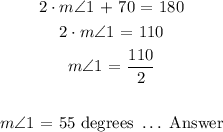Question

Andrew constructed a triangle so that the measurement of 1 and 2 were congruent. if angle 3 measured 70 degrees, what is the measure of angle 1?

Answer 1

Andrew constructed a triangle such that the measurements of angles m<1 and m<2 are congruent.

The above statement can be inferred from concept of congruency of triangles. The oppsoite sides of the two congruent angles in a traingles are also equal.

From the above statement we can deduce the type of a triangle that Andrew drew as follows:

`\text{Andrew drew a isoceles triangle}`

An isoceles triangle has two equal sides and angles i.e congruent sides and interior angles. Hence,

`m\angle1\text{ = m}\angle2\ldots\text{ Eq1}`

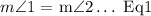
The following information is given for the third interior angle m<3 of the isoceles triangle:

`m\angle3\text{ = 70 degrees}`

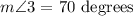
We need determine the angle measure of the angle 1. Recall that the sum of interior angles of a triangle is given as follows:

`m\angle1\text{ + m}\angle2\text{ + m}\angle3\text{ = 180 degrees }\ldots\text{ Eq2}`

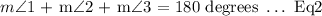
Substitute Eq1 into Eq2 as follows:

`\begin{gathered} m\angle1\text{ + m}\angle1\text{ + m}\angle3\text{ = 180} \\ \\ 2\cdot m\angle1\text{ + m}\angle3\text{ = 180} \end{gathered}`

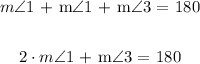
Substitute the angle measurement of angle ( 3 ) in the expression above and solve for angle ( 1 ) as follows:

`\begin{gathered} 2\cdot m\angle1\text{ + 70 = 180} \\ 2\cdot m\angle1\text{ = 110} \\ m\angle1\text{ = }(110)/(2) \\ \\ m\angle1\text{ = 55 degrees }\ldots\text{ Answer} \end{gathered}`