Question

Solve the equation 3x^2 - 5x + 1 = 0 expressing your answer correct to two decimal places

Answer 1

You have th following equation;

`3x^2-5x+1=0`

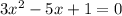
In order to find the solution to the previous equation, use the quadratic formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

In this case, a = 3, b = -5 and c = 1. By replacing these values into the quadratic formula, you obtain:

`\begin{gathered} x=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(3)(1)}}{2(1)} \\ x=\frac{5\pm\sqrt[]{25-12}}{2}=\frac{5\pm\sqrt[]{13}}{2} \\ x=(5\pm3.60)/(2)=2.5\pm1.80 \end{gathered}`

Hence, the solutions are:

x = 2.5 + 1.80 = 4.30

x = 2.5 - 1.80 = 0.70