You need to determine which line is perpendicular to the line

For two lines to be considered perpendicular their slopes must be the inverse positive, that is, if, for example, you have the lines
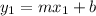
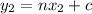
For them to be perpendicular one slope must be the inverse negative of the other such as

The first step is to write the given line in slope-intercept form:
1) Pass the x term to the right side of the equal sign
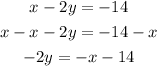
2) Divide both sides of the expression by "-2"
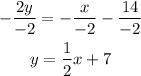
The slope of the line is
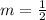
So the slope of a line perpendicular to it will be the inverse negative of it
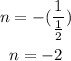
The correct option is the one that has slope -2