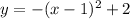Answer:
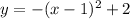
Explanation:
A quadratic function in vertex form is represented as:
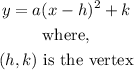
Given the vertex (1,2) substitute it into the function:
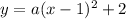
As you can see, we still do not know the value for ''a'', use the point given (4,-7) substitute it (x,y) and solve for ''a'':
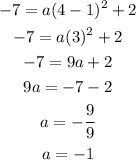
Hence, the equation of the function would be: