Question

What is the solution to the equation below?A.x = -1B.x = 0C.x = -5D.x = 3

Answer 1

Step-by-step explanation

We must solve the following equation for x:

`x+3=√(3-x)`

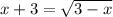
We can square both sides of the equation so we can get rid of the radical:

`\begin{gathered} (x+3)^2=(√(3-x))^2 \\ (x+3)^2=3-x \end{gathered}`

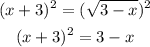
We expand the squared binomial on the left:

`\begin{gathered} (x+3)^2=x^2+6x+9=3-x \\ x^2+6x+9=3-x \end{gathered}`

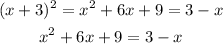
Then we substract (3-x) from both sides:

`\begin{gathered} x^2+6x+9-(3-x)=x-3-(3-x) \\ x^2+6x+9+x-3=0 \\ x^2+7x+6=0 \end{gathered}`

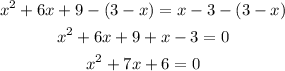
Then we have to find the solutions to this last equation. Remember that the solutions to an equation of the form ax²+bx+c have the form:

`x=(-b\pm√(b^2-4ac))/(2a)`

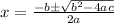
In our case a=1, b=7 and c=6 so we get:

`\begin{gathered} x=(-7\pm√(7^2-4\cdot1\cdot6))/(2\cdot1)=(-7\pm√(49-24))/(2)=(-7\pm√(25))/(2)=(-7\pm5)/(2) \\ x=(-7+5)/(2)=-1\text{ and }x=(-7-5)/(2)=-6 \end{gathered}`

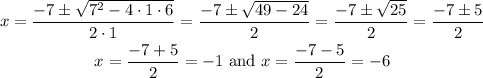
So we have two potential solutions x=-1 and x=-6. However we should note something important, in the original equation we have the term:

`√(3-x)`

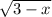
Remember that the result of the square root is always positive. Then the term in the left of the expression has to be positive or 0. Then we impose a restriction in the value of x:

`x+3\ge0\rightarrow x\ge-3`

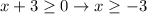
From the two possible solutions only x=-1 is greater than or equal to -3 so this is the correct one.

Answer

Then the answer is option A.