Step-by-step explanation
We must solve the following equation for x:
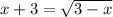
We can square both sides of the equation so we can get rid of the radical:
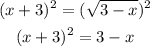
We expand the squared binomial on the left:
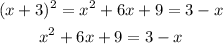
Then we substract (3-x) from both sides:
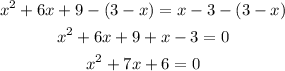
Then we have to find the solutions to this last equation. Remember that the solutions to an equation of the form ax²+bx+c have the form:

In our case a=1, b=7 and c=6 so we get:
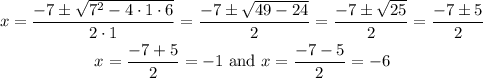
So we have two potential solutions x=-1 and x=-6. However we should note something important, in the original equation we have the term:
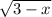
Remember that the result of the square root is always positive. Then the term in the left of the expression has to be positive or 0. Then we impose a restriction in the value of x:
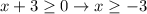
From the two possible solutions only x=-1 is greater than or equal to -3 so this is the correct one.
Answer
Then the answer is option A.