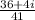Find the quotient given below:
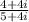
When managing complex numbers, we must recall:

Multiply and divide the expression by the conjugate of the denominator:

Multiply the expressions in the numerator and in the denominator. We can apply the special product formula in the denominator:

Operating:
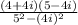
Operate and simplify:
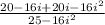
Applying the property mentioned above:
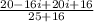
Simplifying: