Question

A=1.9 in, A=46.5°, C=90°Solve the right triangle. Round side lengths one decimal place.

Answer 1

Given the following

`a=1.9in,A=46.5^0,C=90^0`

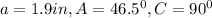
Consider the image below

To solve the right triangle, we need to find the following:

`b=\text{?,c}=\text{?and B=?}`

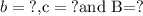
To find B, we use the sum of angles in a triangle

hence

`\begin{gathered} A^0+B^0+C^0=180^0^{} \\ \text{where A=46.5}^0,C=90^0 \end{gathered}`

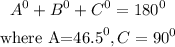
Substituting into the equation we have,

`\begin{gathered} 46.5^0+B+90^0=180^0 \\ 136.5+B=180^0 \end{gathered}`

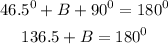
Subtract 136.5 from both sides

`\begin{gathered} 136.5+B-136.5^0=180^0-136.5^0 \\ \text{Then} \\ B=180^0-136.5 \\ B=43.5^0 \end{gathered}`

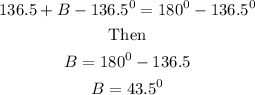
hence

B = 43.5°

To find b, we use the trigonometry ratio for tangent

From the triangle above

`\begin{gathered} \tan A=(a)/(b) \\ \text{Where A=46.5in, a=1.9in, b=?} \end{gathered}`

Substituting into the equation

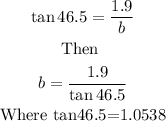
`\begin{gathered} \tan 46.5=(1.9)/(b) \\ \text{Then } \\ b=(1.9)/(\tan46.5) \\ \text{Where tan46.5=1.0538} \end{gathered}`

Then

`b=1.8030`

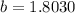
hence

b = 1.8in to 1 decima place

To find c, we also apply trigonometry ratio for sine of an angle

`\begin{gathered} \text{sinA}=\frac{opposite}{\text{hypotenuse}} \\ \text{Where } \\ A=46.5^0,\text{ opposite =1.9in},\text{ hypotenuse =c} \end{gathered}`

Substituting the values into the equation we have,

`\begin{gathered} \sin 46.5=(1.9)/(c) \\ Multiply\text{ both sides by c, we have } \\ c*\sin 46.5=(1.9)/(c)* c \\ \text{Then } \\ c*\sin 46.5=1.9 \end{gathered}`

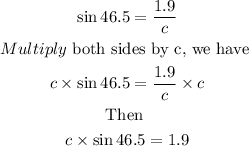
Divide both sides by 1.9, we have

`\begin{gathered} c=(1.9)/(\sin 46.5)=(1.9)/(0.7254) \\ \text{Then} \\ c=2.6193 \end{gathered}`

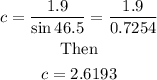
hence

c = 2.6 in

Therefore, to solve the right triangle, we have

Answer; B = 43.5°, b = 1.8in, c = 2.6 in