Question

A convex spherical mirror has a radius of curvatureof 9 40 cm. A) Calculate the location of the image formed by an 7.75mm tall object whose distance from the mirror is 17.5 cmCalculate the size of the imageC) Calculate the location of the image formed by an 7.75mm tall object whose distance from the mirror is 10.0cmE) Calculate the location of the image formed by an 7.75mm tall object whose distance from the mirror is 2.65cmG) Calculate the location of the image formed by an 7.75mm tall object whose distance from the mirror is 9.60m

Answer 1

0.We are asked to determine the location of an image formed by an 7.75mm tall object that is located a distance of 17.5 cm from a convex mirror.

First, we will calculate the focal length using the following formula:

`f=-(R)/(2)`

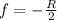
Where:

`\begin{gathered} f=\text{ focal length} \\ R=\text{ radius} \end{gathered}`

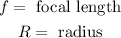
Substituting the values we get:

`f=-(9.40cm)/(2)`

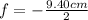
Solving the operations:

`f=-4.7cm`

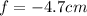
Now, we use the following formula:

`(1)/(d_o)+(1)/(d_i)=(1)/(f)`

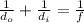
Where:

`\begin{gathered} d_0=\text{ distance of the object} \\ d_i=\text{ distance of the image} \end{gathered}`

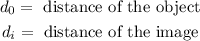
Now, we substitute the known values:

`(1)/(17.5cm)+(1)/(d_i)=-(1)/(4.7cm)`

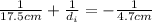
Now, we solve for the distance of the image. First, we subtract 1/17.5 from both sides:

`(1)/(d_i)=-(1)/(4.7cm)-(1)/(17.5cm)`

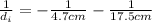
Solving the operation:

`(1)/(d_i)=-0.27(1)/(cm)`

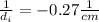
Now, we invert both sides:

`d_i=(1)/(-0.27)cm=-3.7cm`

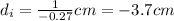
Therefore. the location of the image is -3.7 centimeters.

The other parts are solved using the same procedure.

Part B. To calculate the size of the image we will use the following relationship:

`(h_i)/(h_o)=-(d_i)/(d_0)`

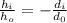
Where:

`h_i,h_0=\text{ height of the image and height of the object}`

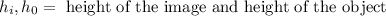
Substituting we get:

`(h_i)/(7.75mm)=-(-3.7cm)/(17.5cm)`

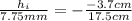
Solving the operations on the right side:

`(h_i)/(7.75mm)=0.21`

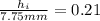
Now, we multiply both sides by 7.75:

`h_i=(7.75mm)(0.21)`

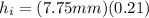
Solving the operations:

`h_i=1.64mm`

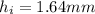
Therefore, the height of the iamge is 1.64 mm.