The first step to factor this expression is to find its roots (the values of 'n' that makes this expression equals zero)
To find the roots, we can use the quadratic formula:
(Using the coefficients a=2, b=7 and c=5)
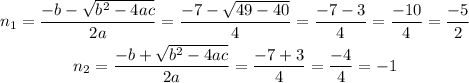
So the roots of the expression are -5/2 and -1. Now, we can write the expression in this factored form:

So the factored form is (2n+5)(n+1)