Given: The expression below
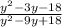
To Determine: The lowest term of the given rational fraction
Solution
Let simplify both the numerator and the denominator
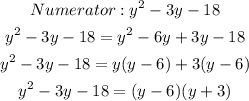

Therefore
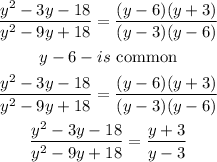
Hence, the rational expression in its lowest term is
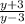
The variable for the original expression is as given as
