Question

Find equation of line containing the given points (4,3) and (8,0) Write equation in slope-intercept form

Answer 1

Write out the given point

`\begin{gathered} (4,3) \\ \text{and } \\ (8,0) \end{gathered}`

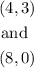
The equation of the line passing through the point above will be obtain by following the steps

Step1: Obtain the slope of the line

`\begin{gathered} \text{slope,m}=(y_2-y_1)/(x_2-x_1) \\ \text{Hence } \\ x_1=4,x_2=8 \\ y_1=3,y_2=0 \end{gathered}`

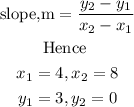
Substituting the values we have

`\begin{gathered} \text{slope,m}=(0-3)/(8-4)=-(3)/(4) \\ \text{Hence } \\ m=-(3)/(4) \end{gathered}`

Step 2: Obtain the y- intercept

The y-intercept is the point where the graph touch the y, axis

`\begin{gathered} \text{slope, m=-3/4} \\ y=6 \\ y-intercept=6 \end{gathered}`

Steps 3; use the slope intercept rule

`\begin{gathered} y=mx+b \\ \text{Where m=-3/4,b=y-intercept} \\ \text{Then } \\ y=-(3)/(4)x+6 \end{gathered}`

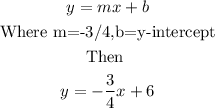
Hence

The equation in slope intercept form is

y = - 3/4 x + 6