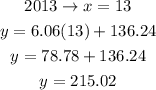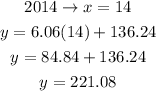Question

The Consumer Price Index (CPI), which measures the cost of a typical package of consumer goods, was 202.9 in 2011 and 233.2 in 2016. Let x=11 correspond to the year 2011 and estimate the CPI in 2013 and 2014. Assume that the data can be modeled by a straight line and that the trend continues indefinitely. Use two data points to find such a line and then estimate the requested quantities. Let y represent the CPI. The linear equation that best models the CPI is____ (Simplify your answer. Use integers or decimals for any numbers in the equation. Round to the nearest hundredth as needed.)

Answer 1

The first thing we have to identify in our problem are the variables

`\begin{gathered} x\to\text{time} \\ y\to\text{CPI} \end{gathered}`

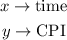
Now we see the points (x,y) that gives us the problem

`\begin{gathered} 2011\to(11,202.9) \\ 2016\to(16,233.2) \end{gathered}`

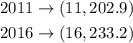
Since behavior can be modeled by a straight line, we use the general equation of the straight line

`y=mx+b`

Where m is the slope of the line and b is the y-intercept.

Taking this into account and with the 2 points that they give us, we proceed to calculate the equation of the line starting with the slope:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(233.2-202.9)/(16-11) \\ m=(30.3)/(5) \\ m=6.06 \end{gathered}`
`\begin{gathered} y=6.06x+b \\ 202.9=6.06(11)+b \\ b=202.9-66.66 \\ b=136.24 \end{gathered}`

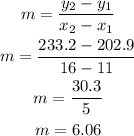
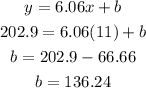
The equation that models the behavior of the CPI is

`y=6.06x+136.24`

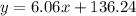
Now we calculate the CPI values for the years 2013 and 2014

`\begin{gathered} 2013\to x=13 \\ y=6.06(13)+136.24 \\ y=78.78+136.24 \\ y=215.02 \end{gathered}`
`\begin{gathered} 2014\to x=14 \\ y=6.06(14)+136.24 \\ y=84.84+136.24 \\ y=221.08 \end{gathered}`