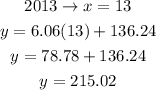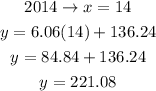The first thing we have to identify in our problem are the variables
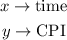
Now we see the points (x,y) that gives us the problem
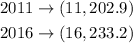
Since behavior can be modeled by a straight line, we use the general equation of the straight line
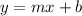
Where m is the slope of the line and b is the y-intercept.
Taking this into account and with the 2 points that they give us, we proceed to calculate the equation of the line starting with the slope:
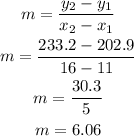
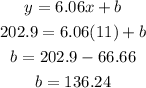
The equation that models the behavior of the CPI is
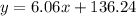
Now we calculate the CPI values for the years 2013 and 2014