Question

Please explain in depth. Thank you in advance for a response.

Answer 1

We have the function:

`y=f(t)=(-18t-3)\cdot(t-2).`

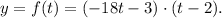
a. Zeros of the function

By definition, the zeros are the values of t such that f(t) = 0. In this case, we have:

`f(t)=(-18t-3)\cdot(t-2)=0\text{.}`

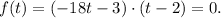
Rewriting the function, we have:

`f(t)=(-18)\cdot(t+(1)/(6))\cdot(t-2)=0.`

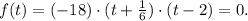
So the zeros of the function are:

`\begin{gathered} t=-(1)/(6), \\ t=2. \end{gathered}`

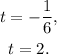
b. Meaning of the zeros

The function y = f(t) represents the height of the ball at time t.

• So the zeros are the times at which the function reaches a height equal to zero.

,

• We see that one zero is positive and the other negative. Only the positive zero (t = 2) is meaningful because the negative (t = -1/6) represents a negative value of time!

c. Initial height

The ball is thrown at time t = 0. The height of the ball at time t = 0 is:

`y=f(0)=(-18\cdot0-3)\cdot(0-2)=(-3)\cdot(-2)=6.`

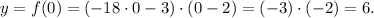
So the ball is thrown from a height of 6 feet.

Answer

• a., The zeros are t = -1/6 and t = 2.

,

• b., The zeros are the values of time at which the height of the ball is zero. Only a positive value of time makes sense, so only the zero t = 2 is meaningful.

,

• c., The ball is thrown from a height of 6 feet.