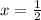Let us start with the following quadratic function:
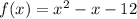
the X-intercepts are the collection of values to X which makes f(x) = 0, and it can be calculated by the Bhaskara formula:
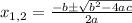
where the values a, b, and c are given by:

Substituting the values from the proposed equation, we have:
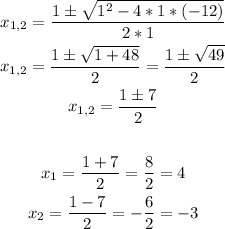
From the above-developed solution, we are able to conclude that the solution for the first box is:
(-3,0) ,(4,0)
Now, the y-intercept, is just the value of y when x = 0, which can be calculated as follows:
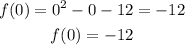
From this, we are able to conclude that the solution for the second box is:
(0, -12)
Now, the vertex is the value of minimum, or maximum, in the quadratic equation, and use to be calculated as follows:
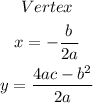
substituting the values, we have:
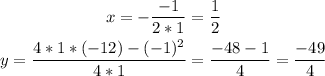
which means that the solution for the thirst box is:
(1/2, -49/4) (just as in the photo)
Now, the line of symmetry equation of a quadratic function is a vertical line that passes through the vertex, which was calculated to be in the point: (1/2, -49,4).
Because this is a vertical line, it is represented as follows: