Question

In the triangle below, suppose that mV = (x - 2)",mW = (x - 2)°, and m ZX=(4x+4)*Find the degree measure of each angle in the triangle.(x - 2)(4x + 4)m ZV =Х5?m ZW =001Xm 2x =(x - 2)°

Answer 1

Consider the image given below.

From the image above,

`\begin{gathered} \angle V=(x-2)^0 \\ \angle W=(x-2)^0 \\ \angle X=(4x+4)^0 \end{gathered}`

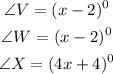
To find the measures of each angle, we need to obtain the value of small x in the diagram.

Applying the rule: Sum of angle in a triangle is 180 degrees

`\angle V+\angle W+\angle X=180^0`

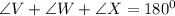
Then substitute the given expression, we have

`\begin{gathered} (x-2)^0+(x-2)^0+(4x+4)^0=180^0 \\ Then \\ x-2+x-2+4x+4=180^0 \end{gathered}`

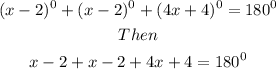
Collect like terms and add

`\begin{gathered} x+x+4x-2-2+4=180^0 \\ 6x-4+4=180^0 \\ \text{then} \\ 6x=180 \end{gathered}`

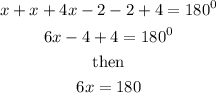
Divide both sides by 6, we have

`\begin{gathered} (6x)/(6)=(180)/(6) \\ hence \\ x=30 \end{gathered}`

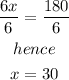
hence, x=30

Then substitute the value of x to obtain the measure of each angles.

`\begin{gathered} \angle V=(x-2)^0 \\ \text{Then x=30} \\ \angle V=30-2=28^0 \end{gathered}`

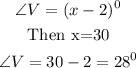
Since the triangle is an issoceles triangle, then

`\angle W=28^0`

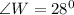
Hence

`\begin{gathered} \angle X=(4x+4)^0 \\ \angle X=(4*30+4)^0=(120+4)=124^0 \\ \text{hence} \\ \angle X=124^0 \end{gathered}`

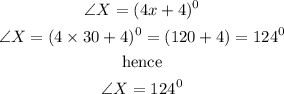
Therefore

Answer : ∠V= 28°, ∠W=28°, ∠X=124°