1 Answer

Jeremy Gwa · Answer 1 · 2023-05-01T17:23:13+0000

SOLUTION

Consider the image given below.

From the image above,

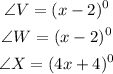
$\begin{gathered} \angle V=(x-2)^0 \\ \angle W=(x-2)^0 \\ \angle X=(4x+4)^0 \end{gathered}$

To find the measures of each angle, we need to obtain the value of small x in the diagram.

Applying the rule: Sum of angle in a triangle is 180 degrees

$\angle V+\angle W+\angle X=180^0$

Then substitute the given expression, we have

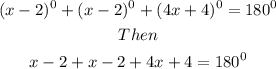
$\begin{gathered} (x-2)^0+(x-2)^0+(4x+4)^0=180^0 \\ Then \\ x-2+x-2+4x+4=180^0 \end{gathered}$

Collect like terms and add

$\begin{gathered} x+x+4x-2-2+4=180^0 \\ 6x-4+4=180^0 \\ \text{then} \\ 6x=180 \end{gathered}$

Divide both sides by 6, we have

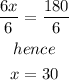
$\begin{gathered} (6x)/(6)=(180)/(6) \\ hence \\ x=30 \end{gathered}$

hence, x=30

Then substitute the value of x to obtain the measure of each angles.

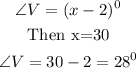
$\begin{gathered} \angle V=(x-2)^0 \\ \text{Then x=30} \\ \angle V=30-2=28^0 \end{gathered}$

Since the triangle is an issoceles triangle, then

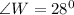
$\angle W=28^0$

Hence

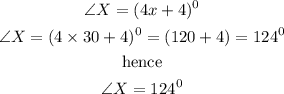
$\begin{gathered} \angle X=(4x+4)^0 \\ \angle X=(4*30+4)^0=(120+4)=124^0 \\ \text{hence} \\ \angle X=124^0 \end{gathered}$

Therefore

Answer : ∠V= 28°, ∠W=28°, ∠X=124°

Please log in or register to add a comment.