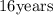Question

The rate of growth of a particular population is given by dP/dt=50t^2-100t^3/2, where P is population size and t is fine and years. Assume the initial population is 25,000. a) determine the population function, P(t)b) estimate to the nearest year how long it will take for the population to reach 50,000

Answer 1

Step1: write out the giving equation

`(dp)/(dt)=50t^2-100t^{(3)/(2)}`

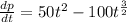
Step2: Integrate both sides of the equation above

`\int (dp)/(dt)=\int 50t^2dt-\int 100t^{(3)/(2)}dt`

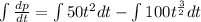
Then simplify by integrating both sides

`p(t)=(50t^(2+1))/(2+1)-\frac{100t^{(3)/(2)+1}}{(3)/(2)+1}+c`
`p(t)=(50)/(3)t^3-40t^{(5)/(2)}+c`

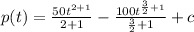
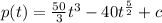
since the initial value is 25,000, then

the Population function is

`\begin{gathered} p(t)=(50)/(3)t^3-40t^{(5)/(2)}+25000\ldots\ldots..\ldots\text{.. is the population function} \\ \text{where t=time in years} \end{gathered}`

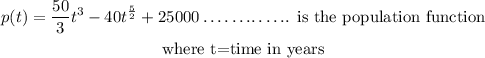
b). For the population to reach 50,000 the time will be

`\begin{gathered} 50000=(50)/(3)t^3-40t^{(5)/(2)}+2500 \\ 50000-25000=(50)/(3)t^3-40t^{(5)/(2)} \\ 25000=(50)/(3)t^3-40t^{(5)/(2)} \\ \text{Then} \\ (50)/(3)t^3-40t^{(5)/(2)}-25000=0 \\ \end{gathered}`

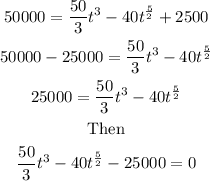
Multiply the equation by 3, we have

`\begin{gathered} 50t^3-120t^{(5)/(2)}-75000=0 \\ \end{gathered}`

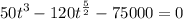
To solve this we rewrite the function as

`14400t^5=\mleft(-50t^3+75000\mright)^2`

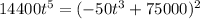
The value of t becomes

`\begin{gathered} t\approx\: 15.628,\: t\approx\: 9.443 \\ t=15.625\text{ satisfy the equation above } \end{gathered}`

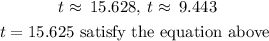
Then it will take approximately

`16\text{years}`