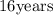SOLUTION
Step1: write out the giving equation
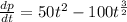
Step2: Integrate both sides of the equation above

Then simplify by integrating both sides
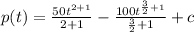
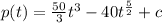
since the initial value is 25,000, then
the Population function is
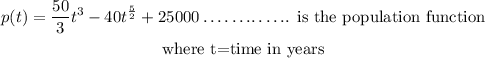
b). For the population to reach 50,000 the time will be
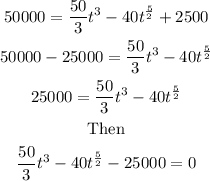
Multiply the equation by 3, we have
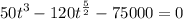
To solve this we rewrite the function as
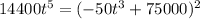
The value of t becomes

Then it will take approximately