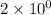Solution:
Let the two numbers be
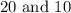
In scientific notation, the numbers are
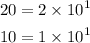
The sum of the numbers will be
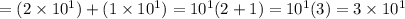
Hence, the sum is
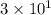
The difference between the two numbers will be
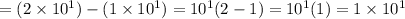
Hence, the difference is
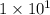
The product of the numbers will be
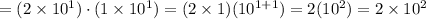
Hence, the product is
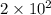
The quotient of the numbers will be
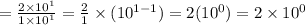
Hence, the quotient is