In a unit circle, given the (x,y) coordinate, x corresponds to cosine, and y corresponds to sine.
Then use the trigonometric identity to solve for tangent.
We therefore have the following ratios for sin, cos, and tan.
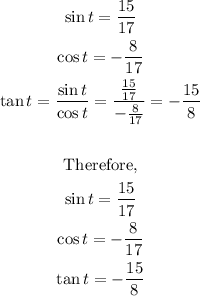
Solving for the reciprocal of sin, cos, and tan we have
